BẢNG BĂM (HASH TABLE)
Phép
băm được đề xuất và hiện thực trên máy tính từ những năm 50 của thế kỷ 20. Nó
dựa trên ý tưởng: biến đổi giá trị khóa thành một số (xử lý băm) và sử dụng số
này để đánh chỉ cho bảng dữ liệu.
 Các
phép toán trên các cấu trúc dữ liệu như danh sách, cây nhị phân,… phần lớn được
thực hiện bằng cách so sánh các phần tử của cấu trúc, do vậy thời gian truy
xuất không nhanh và phụ thuộc vào kích thước của cấu trúc.
Các
phép toán trên các cấu trúc dữ liệu như danh sách, cây nhị phân,… phần lớn được
thực hiện bằng cách so sánh các phần tử của cấu trúc, do vậy thời gian truy
xuất không nhanh và phụ thuộc vào kích thước của cấu trúc.
Trong
bài này chúng ta sẽ khảo sát một cấu trúc dữ liệu mới được gọi là bảng băm (hash
table). Các phép toán trên bảng băm sẽ giúp hạn chế số lần so sánh, và vì vậy
sẽ cố gắng giảm thiểu được thời gian truy xuất. Độ phức tạp của các phép toán
trên bảng băm thường có bậc là 0(1) và không phụ thuộc vào kích thước của bảng
băm.
Các khái niệm chính trên cấu trúc bảng băm:
· Phép băm hay hàm băm (hash function)
· Tập khoá của các phần tử trên bảng băm
· Tập địa chỉ trên bảng băm
· Phép toán thêm phần tử vào bảng băm
· Phép toán xoá một phần tử trên bảng băm
· Phép toán tìm kiếm trên bảng băm
Thông thường bảng băm được sử dụng khi cần xử lý các bài toán có dữ liệu lớn và được lưu trữ ở bộ nhớ ngoài.
1. PHÉP BĂM (Hash Function)
Định nghĩa:
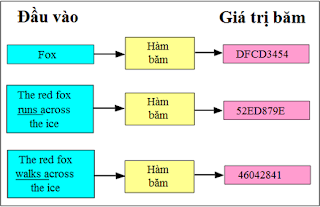
Trong
hầu hết các ứng dụng, khoá được dùng như một phương thức để truy xuất dữ liệu.
Hàm băm được dùng để ánh xạ giá trị khóa khoá vào một dãy các địa chỉ của bảng
băm (hình 1).
Hình 1
Khóa
có thể là dạng số hay số dạng chuỗi. Giả sử có 2 khóa phân biệt ki
và kj nếu h(ki)=h(kj) thì hàm băm bị đụng độ.
Một hàm băm tốt phải thỏa mãn các điều kiện sau:
Tính toán nhanh.
Các khoá được phân bố đều trong bảng.
Ít xảy ra đụng độ.
Xử lý được các loại khóa có kiểu dữ liệu khác
nhau
Hàm Băm sử dụng Phương pháp chia
Dùng số dư: h(k) = k mod m
k là khoá, m là kích thước của bảng.
Như vậy h(k) sẽ nhận:
0,1,2,…,m-1.
Việc chọn m sẽ ảnh hưởng đến
h(k).
Nếu
chọn m=2p thì giá trị của h(k) sẽ là p bit cuối cùng của
k trong biểu diễn nhị phân.
Nếu
chọn m=10p thì giá trị của h(k) sẽ là p chữ số cuối cùng trong biểu
diễn thập phân của k.
Trong
2 ví dụ trên giá trị h(k) không phụ thuộc đầy đủ vào khóa k mà chỉ phụ thuộc
vào p bít (p chữ số) cuối cùng trong
khóa k. Tốt nhất ta nên chọn m sao cho h(k) phụ thuộc đầy đủ và khóa k. Thông
thường chọn m là số nguyên tố.
VD: Bảng băm có 4000 mục, chọn m = 4093
Hàm Băm sử dụng Phương pháp nhân
h(k) = ëm*(k*A mod 1) û
k
là khóa, m là kích thước bảng, A là hằng số: 0 < A < 1
Chọn m và A
Theo
Knuth thì chọn A bằng giá trị sau:
A=( -1)/2=0.6180339887…
-1)/2=0.6180339887…
m thường chọn m = 2p
VD: k=123456; m=10000
H(k)= ë10000 (123456*
0.6180339887 mod 1) û
H(k)= ë10000 (76300.0041089472
mod 1) û
H(k)= ë10000 (0.0041089472) û
H(k)=41
Phép băm phổ quát (unisersal hashing)
Việc chọn hàm băm không tốt có thể
dẫn đến xác suất đụng độ cao.
Giải pháp:
-
Lựa chọn hàm băm h ngẫu nhiên.
-
Khởi tạo một tập các hàm băm H phổ quát và từ đó h được chọn ngẫu nhiên.
Cho
H là một tập hợp hữu hạn các hàm băm: ánh xạ các khóa k từ tập khóa U vào miền
giá trị {0,1,2,…, m-1}. Tập H là phổ quát nếu với mọi " f Î H và 2 khoá phân biệt k1,k2
ta có xác suất: Pr{f(k1) = f(k2)} <= 1/m
2. BẢNG BĂM (Hash Table - Direct-address table)
Phần này sẽ trình bày các vấn đề chính:
- Mô tả cấu trúc bảng băm tổng quát (thông qua hàm băm, tập khóa, tập địa chỉ)
- Các phép toán trên bảng băm như thêm phần tử (insert), loại bỏ (remove), tìm kiếm (search), …
a. Mô tả dữ liệu
Tập khóa
K
Hàm băm
Tập địa chỉ M
Giả sử
· K: tập các khoá (set of keys)
· M: tập các dịa chỉ (set of addresses).
· h(k): hàm băm dùng để ánh xạ một khoá k từ tập các khoá K
thành một địa chỉ tương ứng trong tập M.
b. Các phép toán trên bảng băm
· Khởi tạo (Initialize): Khỏi tạo bảng băm, cấp phát vùng
nhớ hay qui định số phần tử (kích thước) của bảng băm
· Kiểm tra rỗng (Empty): kiểm tra bảng băm có rỗng hay
không?
· Lấy kích thước của bảng băm (Size): Cho biết số phần tử
hiện có trong bảng băm
· Tìm kiếm (Search): Tìm kiếm một phần tử trong bảng băm
theo khoá k chỉ định trước.
· Thêm mới phần tử (Insert): Thêm một phần tử vào bảng băm.
Sau khi thêm số phần tử hiện có của bảng băm tăng thêm một đơn vị.
· Loại bỏ (Remove): Loại bỏ một phần tử ra khỏi bảng băm, và
số phần tử sẽ giảm đi một.
· Sao chép (Copy): Tạo một bảng băm mới tử một bảng băm cũ
đã có.
· Xử lý các khóa trong bảng băm (Traverse): xử lý toàn bộ
khóa trong bảng băm theo thứ tự địa chỉ từ nhỏ đến lớn.
Các Bảng băm thông dụng:
Với mỗi loại
bảng băm cần thiết phải xác định tập khóa K, xác
định tập địa chỉ M và xây dựng hàm băm h cho phù hợp.
*) Bảng băm
với phương pháp kết nối trực tiếp: mỗi địa chỉ của bảng băm tương ứng một danh
sách liên kết. Các phần tử bị xung đột được kết nối với nhau trên một danh sách
liên kết.
*) Bảng băm
với phương pháp kết nối hợp nhất: bảng băm này được cài đặt bằng danh sách kề,
mỗi phần tử có hai trường: trường key chứa khóa của phần tử và trường next chỉ
phần tử kế bị xung đột. Các phần tử bị xung đột được kết nối nhau qua trường kết
nối next.
*) Bảng băm
với phương pháp dò tuần tự: Khi thêm phần tử vào bảng băm nếu bị đụng độ thì sẽ
dò địa chỉ kế tiếp… cho đến khi gặp địa chỉ trống đầu tiên thì thêm phần tử vào
địa chỉ này.
*) Bảng
băm với phương pháp dò bậc hai: ví dụ khi thêm phần tử vào bảng băm này, nếu
băm lần đầu bị xung đột thì sẽ dò đến địa chi mới, ở lần dò thứ i sẽ xét phần tử cách i2
cho đến khi gặp địa chỉ trống đầu tiên thì thêm phần tử vào địa chỉ này.
*) Bảng
băm với phương pháp băm kép: bảng băm này dùng hai hàm băm khác nhau, băm lần
đầu với hàm băm thứ nhất nếu bị xung đột thì xét địa chỉ khác bằng hàm băm thứ
hai.
Ưu điểm của các Bảng băm:
Bảng băm là
một cấu trúc dung hòa giữa thời gian truy xuất và dung lượng bộ nhớ:
- Nếu không
có sự giới hạn về bộ nhớ thì chúng ta có thể xây dựng bảng băm với mỗi khóa ứng
với một địa chỉ với mong muốn thời gian truy xuất tức thời.
- Nếu dung
lượng bộ nhớ có giới hạn thì tổ chức một số khóa có cùng địa chỉ, khi đó tốc độ
truy xuất sẽ giảm.
Bảng băm dược
ứng dụng nhiều trong thực tế, rất thích hợp khi tổ chức dữ liệu có kích thước
lớn và được lưu trữ ở bộ nhớ ngoài.
3. Các phương pháp tránh xảy ra đụng độ
2.4.1. Bảng băm với phương pháp kết nối trực tiếp (Direct chaining Method)
Bảng băm được
cài đặt bằng các danh sách liên kết, các phần tử trên bảng băm được “băm” thành
M danh sách liên kết (từ danh sách 0 đến danh sách M–1). Các phần tử bị xung
đột tại địa chỉ i được kết nối trực tiếp với nhau qua danh sách liên kết i. Chẳng hạn, với M=10, các phần tử có
hàng đơn vị là 9 sẽ được băm vào danh sách liên kết i = 9.
Khi thêm một
phần tử có khóa k vào bảng băm, hàm băm f(k) sẽ xác định địa chỉ i trong khoảng
từ 0 đến M-1 ứng với danh sách liên kết i mà phần tử này sẽ được thêm vào.
Khi tìm một
phần tử có khóa k vào bảng băm, hàm băm f(k) cũng sẽ xác định địa chỉ i trong
khoảng từ 0 đến M-1 ứng với danh sách liên kết i có thể chứa phần tử này. Như
vậy, việc tìm kiếm phần tử trên bảng băm sẽ được qui về bài toán tìm kiếm một
phần tử trên danh sách liên kết.
Để minh họa ta xét bảng băm có cấu trúc như sau:
- Tập khóa K: tập số tự nhiên
- Tập địa chỉ M: gồm 10 địa chỉ (M={0, 1, …, 9}
- Hàm băm h(key) = key % 10.30, 50,60,11,21,31,…
Hình 1.6.
bảng băm với phương pháp kết nối trực tiếp
Hình trên
minh họa bảng băm vừa mô tả. Theo hình vẽ, bảng băm đã "băm" phần tử
trong tập khoá K theo 10 danh sách liên kết khác nhau, mỗi danh sách liên kết
gọi là một bucket:
· Bucket 0 gồm những phần tử có khóa tận cùng bằng 0.
· Bucket i(i=0 | … | 9) gồm những phần tử có khóa tận cùng
bằng i.
· Khi khởi động bảng băm, con trỏ đầu của các bucket là
NULL.
Theo cấu trúc
này, với tác vụ insert, hàm băm h(k) sẽ được dùng để tính địa chỉ của khoá k,
tức là xác định bucket chứa phần tử và đặt phần tử cần chèn vào bucket này.
Với tác vụ
search, hàm băm sẽ được dùng để tính địa chỉ và tìm phần tử trên bucket tương
ứng
+ i=h(k) => thuoc danh sach thu I (bucket[i]
+ tim kiem
khoa K tren danh sach bucket[i]
Cài đặt bảng băm dùng phương pháp kết nối trực tiếp :
a. Khai báo cấu trúc bảng băm:
#define M 100
struct nodes
{ int key;
struct nodes *next };
typedef struct nodes *NODEPTR; //khai bao kieu con tro chi
nut
/*khai bao mang bucket chua M con tro dau cua Mbucket */
NODEPTR bucket[M];
BT: xay dung bang bam theo PP ket noi truc tiep
|
b.Các phép toán:
- Tính giá trị hàm
băm: Giả sử chúng ta chọn hàm băm dạng %: h(key)=key
% M.
- Phép toán initbuckets: khởi tạo các bucket băng Null.
- Phép toán emmptybucket(b): kiểm tra bucket b có bị rỗng
không?
- Phép toán emmpty: Kiểm tra bảng băm có rỗng không?
- Phép toán insert: Thêm phần tử có khóa k vào bảng băm.
+ i=h(k)
+ ktra bucket
[i]: neu rong =>cc o nho cho bucket, gan khoa k
them phan tu co khoa k vao ds theo thu
tu tang dan.
- Phép toán remove: Xóa phần tử có khóa k trong bảng băm.
- Phép toán clear: Xóa tất cả các phần tử trong bảng băm.
- Phép toán traversebucket: Xử lý tất cả các phần tử trong
bucket b.
- Phép toán traverse: Xử lý tất cả các phần tử trong bảng
băm.
- Phép toán search: Tìm
kiếm một phần tử trong bảng băm, nếu không tìm thấy hàm này trả về hàm NULL, nếu
tìm thấy hàm này trả về địa chỉ của phần tử có khóa k.
B1: Tìm danh
sách liên kết có thể chứa khóa k
b = h(k); p = bucket[b];
B2: Tìm khóa
k trong danh sách liên kết p.
Nhận xét bảng băm dùng phương pháp kết nối trực tiếp:
Bảng băm dùng
phương pháp kết nối trực tiếp sẽ "băm” n phần tử vào danh sách liên kết (M
bucket).
Để tốc độ
thực hiện các phép toán trên bảng hiệu quả thì cần chọn hàm băm sao cho băm đều
n phần tử của bảng băm cho M bucket, lúc này trung bình mỗi bucket sẽ có n/M
phần tử. Chẳng hạn, phép toán search sẽ thực hiện việc tìm kiếm tuần tự trên
bucket nên thời gian tìm kiếm lúc này có bậc 0(n/M) – nghĩa là, nhanh gấp M lần
so với việc tìm kiếm trên một danh sách liên kết có n phần tử.
Nếu chọn M
càng lớn thì tốc độ thực hiện các phép toán trên bảng băm càng nhanh, tuy nhiên
lại càng dùng nhiều bộ nhớ. Do vậy, cần điều chỉnh M để dung hòa giữa tốc độ
truy xuất và dung lượng bộ nhớ.
· Nếu chọn M=n thì năng xuất tương đương với truy xuất trên
mảng (có bậc O(1)), tuy nhiên tốn nhiều bộ nhớ.
2.4.2. Bảng băm với phương pháp kết nối hợp nhất
Mô tả:
- Cấu trúc dữ liệu: Tương tự như trong trường hợp cài đặt
bằng phương pháp kết nối trực tiếp, bảng băm trong trường hợp này được cài đặt
bằng danh sách liên kết dùng mảng, có M phần tử. Các phần tử bị xung đột tại
một địa chỉ được kết nối nhau qua một danh sách liên kết. Mỗi phần tử của bảng
băm gồm hai trường:
· Trường key: chứa khóa của mỗi
phần tử
· Trường next: con trỏ chỉ đến phần
tử kế tiếp nếu có xung đột.
- Khởi động: Khi khởi động, tất cả trường key của các phần
tử trong bảng băm được gán bởi giá trị NullKey, còn tất cả các trường next được
gán –1.
- Thêm mới một phần tử: Khi thêm mới một phần tử có khóa key
vào bảng băm, hàm băm hkey) sẽ xác định địa chỉ i trong khoảng từ 0 đến M-1.
· Nếu chưa bị
xung đột thì thêm phần tử mới vào địa chỉ này.
· Nếu bị xung
đột thì phần tử mới được cấp phát là phần tử trống phía cuối mảng. Cập nhật
liên kết next sao cho các phần tử bị xung đột hình thành một danh sách liên
kết.
- Tìm kiếm: Khi tìm kiếm một phần tử có khóa key trong bảng
băm, hàm băm h(key) sẽ giúp giới hạn phạm vi tìm kiếm bằng cách xác định địa
chỉ i trong khoảng từ 0 đến M-1, và việc tìm kiếm phần tử khóa có khoá key
trong danh sách liên kết sẽ xuất phát từ địa chỉ i.
Để minh họa cho bảng băm với phương pháp kết nối hợp nhất,
xét ví dụ sau:
Giả sử, khảo sát bảng băm có cấu trúc như sau:
- Tập khóa K: tập số tự nhiên
- Tập địa chỉ M: gồm 10 địa chỉ (M={0, 1, …, 9}
- Hàm băm f(key) = key % 10.
VD:
Key : 11 12 21 1 13
Hash: 1 2 1 1 3
Add
|
Key
|
Next
|
Add
|
Key
|
Next
|
|
0
|
NullKey
|
-1
|
0
|
NullKey
|
-1
|
|
1
|
NullKey
|
-1
|
1
|
11
|
9
|
|
…
|
NullKey
|
-1
|
2
|
12
|
-1
|
|
M-1
|
NullKey
|
-1
|
3
|
13
|
-1
|
|
…
|
NullKey
|
-1
|
||||
8
|
1
|
-1
|
||||
9
|
21
|
8
|
Khai báo cấu trúc bảng băm:
#define NULLKEY –1
#define M 100
typedef struct node
{
int key; //khoa cua nut tren bang bam
int next; //con tro chi nut ke tiep khi co xung dot
} NODE;
NODE hashtable[M]; //Khai bao bang bam
Cài đặt bảng băm dùng phương pháp kết nối hợp nhất:
2.4.3. Bảng băm với phương pháp dò tuần tự
Mô tả:
- Cấu trúc dữ liệu: Bảng băm trong trường hợp này được cài
đặt bằng danh sách kề có M phần tử, mỗi phần tử của bảng băm là một mẫu tin có
một trường key để chứa khoá của phần tử. Khi khởi động bảng băm thì tất cả
trường key được gán NullKey;
- Khi thêm phần tử có khoá key vào bảng băm, hàm băm h(key)
sẽ xác định địa chỉ i trong khoảng từ 0 đến M-1:
· Nếu chưa bị
xung đột thì thêm phần tử mới vào địa chỉ này.
· Nếu bị xung
đột thì hàm băm lại lần 1, hàm h1 sẽ xét địa chỉ kế tiếp, nếu lại bị xung đột
thì hàm băm thì hàm băm lại lần 2, hàm h2 sẽ xét địa chỉ kế tiếp nữa, …, và quá
trình cứ thế cho đến khi nào tìm được địa chỉ trống và thêm phần tử mới vào địa
chỉ này.
- Khi tìm một
phần tử có khoá key trong bảng băm, hàm băm h(key) sẽ xác định địa chỉ i trong
khoảng từ 0 đến M-1, tìm phần tử khoá key trong bảng băm xuất phát từ địa chỉ i.
Hàm băm lại lần i được biểu diễn bằng công thức sau:
f(key)=(f(key)+i) %M với f(key) là hàm băm chính của bảng
băm.
Lưu ý địa chỉ dò tìm
kế tiếp là địa chỉ 0 nếu đã dò đến cuối bảng.
Giả sử, khảo sát bảng băm có cấu trúc như sau:
- Tập khóa K: tập số tự nhiên
- Tập địa chỉ M: gồm 10 địa chỉ (M={0, 1, …, 9}
- Hàm băm h(key) = key % 10.
Hình thể hiện thêm các nut 32, 53, 22, 92, 17, 34, 24, 37,
56 vào bảng băm.
0
|
NULL
|
0
|
NULL
|
0
|
NULL
|
0
|
NULL
|
0
|
56
|
1
|
NULL
|
1
|
NULL
|
1
|
NULL
|
1
|
NULL
|
1
|
NULL
|
2
|
32
|
2
|
32
|
2
|
32
|
2
|
32
|
2
|
32
|
3
|
53
|
3
|
53
|
3
|
53
|
3
|
53
|
3
|
53
|
4
|
NULL
|
4
|
22
|
4
|
22
|
4
|
22
|
4
|
22
|
5
|
NULL
|
5
|
92
|
5
|
92
|
5
|
92
|
5
|
92
|
6
|
NULL
|
6
|
NULL
|
6
|
34
|
6
|
34
|
6
|
34
|
7
|
NULL
|
7
|
NULL
|
7
|
17
|
7
|
17
|
7
|
17
|
8
|
NULL
|
8
|
NULL
|
8
|
NULL
|
8
|
24
|
8
|
24
|
9
|
NULL
|
9
|
NULL
|
9
|
NULL
|
9
|
37
|
9
|
37
|
Khai báo cấu trúc bảng băm:
#define NULLKEY –1
#define M 100
struct node
{
int key; //khoa cua nut tren bang bam
};
struct node hashtable[M]; //Khai bao bang bam co M nut
Cài đặt bảng băm dùng phương pháp dò tuyến tính:
2.4.4. Bảng băm với phương pháp dò bậc hai
Mô tả:
- Bảng băm trong trường hợp này được cài đặt bằng danh sách
kề có M phần tử, mỗi phần tử của bảng băm là một mẫu tin có một trường key để
chứa khóa các phần tử.
- Khi khởi động bảng băm thì tất cả trường key bị gán NULLKEY.
Khi thêm phần tử có khóa key vào bảng băm, hàm băm h(key) sẽ
xác định địa chỉ i trong khoảng từ 0 đến M-1.
· Nếu chưa bị
xung đột thì thêm phần tử mới vào địa chỉ i này.
· Nếu bị xung
đột thì hàm băm lại lần 1 h1 sẽ xét địa chỉ cách i là 12, nếu lại bị
xung đột thì hàm băm lại lần 2 h2 sẽ xét
địa chỉ cách i 22 ,… , quá trình cứ thế cho đến khi nào tìm được
trống và thêm phần tử vào địa chỉ này.
- Khi tìm kiếm một phần tử có khóa key trong bảng băm thì
xét phần tử tại địa chỉ i=f(key), nếu chưa tìm thấy thì xét phần tử cách i 12,
22, …, quá trình cứ thế cho đến khi tìm được khóa (trường hợp tìm
thấy) hoặc rơi vào địa chỉ trống (trường hợp không tìm thấy).
- Hàm băm lại lần thứ i được biểu diễn bằng công thức sau:
fi(key)=( f(key) + i2 ) % M
với f(key) là hàm băm chính của bảng băm.
Nếu đã dò đến cuối bảng thì trở về dò lại từ đầu bảng.
Bảng băm minh họa có cấu trúc như sau:
- Tập khóa K: tập số tự nhiên
- Tập địa chỉ M: gồm 10 địa chỉ (M={0, 1, …, 9}
- Hàm băm f(key) = key % 10.
Khai báo cấu trúc bảng băm:
#define NULLKEY –1
#define M 101
/*
M la so nut co tren bang bam,du de chua cac nut nhap vao
bang bam,chon M la so nguyen to
*/
//Khai bao nut cua bang bam
struct node
{
int key; //Khoa cua nut tren bang bam
};
//Khai bao bang bam co M nut
struct node hashtable[M];
int N;
Cài đặt bảng băm dùng phương pháp dò bậc hai:
Hàm băm: Giả sử chúng
ta chọn hàm băm dạng%: f(key)=key %10.
int hashfunc(int key)
{
return(key% 10);
}
Phép toán initialize
void initialize()
{
int i;
for(i=0; i<M;i++) hashtable[i].key = NULLKEY;
N=0; //so nut hien co khoi dong bang 0
}
Phép toán empty:
int empty()
{
return(N ==0 ?TRUE :FALSE);
}
Phép toán full:
int full()
{
return(N = = M-1 ?TRUE :FALSE);
}
Phép toán search:
Tìm phần tử có khóa k trên bảng băm,nếu không tìm thấy hàm
này trả về trị M, nếu tìm thấy hàm này trả về địa chỉ tìm thấy.
int search(int k)
{
int i, d;
i = hashfuns(k);
d = 1;
while(hashtable[i].key!=k&&hashtable[i].key
!=NULLKEY)
{
//Bam lai (theo phuong phap bac hai)
i = (i+d) % M;
d = d+2;
}
hashtable[i].key =k; N = N+1;
return(i);
}
2.4.5. Bảng băm với phương pháp băm kép
Mô tả:
Phương pháp băm kép dùng hai hàm băm bất kì, ví dụ chọn hai
hàm băm như sau:
h1(key)= key
%M.
h2(key)
=(M-2)-key %(M-2).
Bảng băm trong trường hợp này được
cài đặt bằng danh sách kề có M phần tử, mỗi phần tử của bảng băm là một mẫu tin
có một trường key để lưu khoá các phần tử.
- Khi khởi động bảng băm, tất cả trường key được gán NULLKEY.
- Khi thêm phần tử có khoá key vào bảng băm, thì i=h1(key)
và j=h2(key) sẽ xác định địa chỉ i và j trong khoảng từ 0 đến M-1:
· Nếu chưa bị
xung đột thì thêm phần tử mới tại địa chỉ i này.
· Nếu bị xung
đột thì hàm băm lại lần 1 h1 sẽ xét địa chỉ mới i+j, nếu lại bị xung đột thì
hàm băm lại lần 2 h2 sẽ xét địa chỉ i+2j, …, quá trình cứ thế cho đến khi nào
tìm được địa chỉ trống và thêm phần tử vào địa chi này.
- Khi tìm kiếm một phần tử có khoá key trong bảng băm, hàm
băm i=h1(key) và j=h2(key) sẽ xác định địa chỉ i và j trong khoảng từ 0 đến
M-1. Xét phần tử tại địa chỉ i, nếu chưa tìm thấy thì xét tiếp phần tử i+j, i+2j,
…, quá trình cứ thế cho đến khi nào tìm được khoá (trường hợp tìm thấy) hoặc bị
rơi vào địa chỉ trống (trường hợp không tìm thấy).
Bảng băm dùng
hai hàm băm khác nhau, hàm băm lại của phương pháp băm kép được tính theo hai
giá trị: i (kết quả hàm băm thứ nhất) và j (kết qủa hàm băm thứ hai) theo một
công thức bất kì. Nếu đã dò đến cuối bảng thì trở về dò lại từ đầu bảng.
Bảng băm minh họa có cấu trúc như sau:
- Tập khóa K: tập số tự nhiên
- Tập địa chỉ M: gồm 11 địa chỉ (M={0, 1, …, 10}
- Chọn hàm băm f1(key)=key % 11 và f2(key)=9-key %9.
Khai báo
#define NULLKEY –1
#define M 101 /*M la so nut co tren bang bam,du de chua cac
nut nhap vao bang bam,chon M la so nguyen
to */
struct node
{
int key;//khoa cua nut tren bang bam
};
struct node hashtable[M]; //khai bao bang bam co M nut